Yew Chung International School of Hong Kong geography fieldwork support resources
Resources will continue to be uploaded to this page during July 2018.
River Tordera Data
| SITE 1 | ||||||||
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | Average | |
| Cross-section area (m²) | 0.67 | 0.34 | 0.37 | 0.11 | 0.22 | 0.17 | 0.27 | 0.31 |
| Wetted perimeter (m) | 3.27 | 4.46 | 5.6 | 4.03 | 2.81 | 2.2 | 3.95 | 3.76 |
| Hydraulic radius | 0.205 | 0.08 | 0.07 | 0.5 | 0.08 | 0.08 | 0.07 | 0.16 |
| Velocity (m/sec) | 0.06 | 0.09 | 0.12 | 0.76 | 0.38 | 0.17 | 0.25 | 0.26 |
| Bedload (cms) | 4.73 | 13.03 | 14.91 | 16.97 | 15.71 | 12.04 | 16.05 | 13.35 |
| Gradient (degrees) | 5.75 | 3 | 5 | 1.5 | 3.55 | 4.25 | 3.5 | 3.79 |
| Discharge (m³/sec) | 0.04 | 0.03 | 0.04 | 0.13 | 0.08 | 0.03 | 0.67 | 0.15 |
| Edge radius (cms) | 1.74 | 1.3 | 3.33 | 4.03 | 13.35 | 3.62 | 3.3 | 4.38 |
| Cailleux R value | 735.7 | 199.59 | 496 | 628.23 | 585 | 766.9 | 411.21 | 546.09 |
| SITE 2 | ||||||||
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | Average | |
| Cross-section area (m²) | 1.61 | 1.48 | 1.32 | 0.84 | 0.88 | 1.21 | 1.02 | 1.19 |
| Wetted perimeter (m) | 9.49 | 14 | 13.52 | 4.95 | 8.13 | 10.52 | 10.52 | 10.16 |
| Hydraulic radius | 0.17 | 0.11 | 0.1 | 0.17 | 0.11 | 0.11 | 0.1 | 0.12 |
| Velocity (m/sec) | 0.09 | 0.17 | 0.68 | 0.84 | 0.8 | 0.8 | 0.59 | 0.57 |
| Bedload (cms) | 5.19 | 12.8 | 15.7 | 17.39 | 9.4 | 21.57 | 13.68 | |
| Gradient (degrees) | 2.75 | 2.5 | 6 | 2.9 | 7.5 | 5.75 | 4.25 | 4.52 |
| Discharge (m³/sec) | 0.15 | 0.26 | 0.9 | 0.23 | 0.7 | 0.97 | 0.6 | 0.54 |
| Edge radius (cms) | 2.34 | 1.98 | 3.5 | 5.03 | 3.5 | 3.4 | 3.29 | |
| Cailleux R value | 901.7 | 310 | 489 | 616.5 | 781.8 | 315.25 | 569.04 | |
| SITE 3 | ||||||||
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | Average | |
| Cross-section area (m²) | 1.1 | 0.65 | 0.87 | 0.82 | 1.14 | 0.64 | 1 | 0.89 |
| Wetted perimeter (m) | 6.79 | 6.4 | 6 | 6.15 | 6.97 | 6.8 | 5.05 | 6.31 |
| Hydraulic radius | 0.16 | 0.1 | 0.14 | 0.13 | 0.16 | 0.09 | 0.2 | 0.14 |
| Velocity (m/sec) | 1 | 0.2 | 0.6 | 0.64 | 0.71 | 0.46 | 0.49 | 0.59 |
| Bedload (cms) | 5.48 | 11.67 | 12 | 10.04 | 11.39 | 10.79 | 20.51 | 11.70 |
| Gradient (degrees) | 2.55 | 2 | 5 | 0.87 | 8 | 3 | 2.75 | 3.45 |
| Discharge (m³/sec) | 0.1 | 0.13 | 0.52 | 0.52 | 0.81 | 0.29 | 0.49 | 0.41 |
| Edge radius (cms) | 2.95 | 2.32 | 3.2 | 2.82 | 4.17 | 3.43 | 3.37 | 3.18 |
| Cailleux R value | 1076.6 | 396.93 | 577 | 600 | 760 | 635.77 | 328.19 | 624.93 |
| SITE 4 | ||||||||
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | Average | |
| Cross-section area (m²) | 0.61 | 0.73 | 0.61 | 0.59 | 1.68 | 0.42 | 0.57 | 0.74 |
| Wetted perimeter (m) | 7.22 | 6.3 | 6.6 | 6.3 | 5.37 | 8.33 | 4.24 | 6.34 |
| Hydraulic radius | 0.85 | 0.24 | 0.09 | 0.09 | 0.31 | 0.05 | 0.13 | 0.25 |
| Velocity (m/sec) | 0.26 | 0.36 | 0.45 | 0.72 | 0.22 | 0.36 | 0.64 | 0.43 |
| Bedload (cms) | 4.57 | 9.79 | 8.6 | 3.33 | 7.9 | 14.72 | 8.15 | |
| Gradient (degrees) | 2.25 | 1.33 | 3.33 | 0.47 | 3 | 2.25 | 1.25 | 1.98 |
| Discharge (m³/sec) | 0.16 | 0.26 | 0.27 | 0.43 | 0.37 | 0.15 | 0.36 | 0.29 |
| Edge radius (cms) | 2.17 | 2.02 | 2.8 | 3.28 | 3.3 | 2.82 | 2.73 | |
| Cailleux R value | 949.1 | 411.98 | 780 | 559.1 | 1008 | 382.79 | 681.83 | |
| SITE 5 | ||||||||
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | Average | |
| Cross-section area (m²) | 1.31 | 0.72 | 1.17 | 1.35 | 3.3 | 3.22 | 3.17 | 2.03 |
| Wetted perimeter (m) | 11.64 | 8.7 | 5.4 | 5.9 | 11.05 | 10.7 | 11.71 | 9.30 |
| Hydraulic radius | 0.11 | 0.08 | 0.21 | 0.22 | 0.3 | 0.3 | 0.27 | 0.21 |
| Velocity (m/sec) | 0.25 | 0.22 | 0.56 | 0.45 | 0.08 | 0.08 | 0.08 | 0.25 |
| Bedload (cms) | ||||||||
| Gradient (degrees) | 0.25 | 0.67 | 2 | 0.5 | 1 | 2.5 | 1.75 | 1.24 |
| Discharge (m³/sec) | 0.33 | 0.16 | 0.65 | 0.61 | 0.26 | 0.28 | 0.25 | 0.36 |
| Edge radius (cms) | ||||||||
| Cailleux R value | ||||||||
Spearman's Rank Correlation Coefficient Rs and Probability (p) Value Calculator
The Spearman's Rank Correlation Coefficient Rs value is a statistical measure of the strength of a link or relationship between two sets of data. This calculator generates the Rs value, its statistical significance level based on exact critical probabilty (p) values[1] and the conclusion.
The coefficient (Rs) is calculated using the formula below:
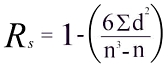
The answer will always be between 1.0 (a perfect positive correlation) and -1.0 (a perfect negative correlation). An Rs of 0 indicates no association between ranks.

The p-value is determined by the observed correlation Rs value and the sample size. The p-value represents the probability that your null hypothesis (that there is no correlation between your data sets) is the correct one. Your hypothesis should always be stated in its null (H0) and alternative (H1) forms. If your p-value is statistically significant, you must reject your null hypothesis and accept the alternative (that there is a correlation between your data sets).
In geography we generally work with a 5% probability level (p = 0.05). This means that the probability of the correlation in the data being caused solely by chance is 5% or less. In other words, there is at least a 95% probability that the data is statistically significant and that it shows a true relationship. In this case, you must reject the null (H0) hypothesis and accept the alternative hypothesis (H1). A 5% (p = 0.05) probability level indicates statistical significance with at least 95 in every 100 researchers undertaking the same investigation expected to draw similar conclusions from their data analysis.
With a large sample size a very weak correlation Rs value can have a significant p-value. In this case, the weak correlation is not due to chance factors, but because with a large sample the low correlation is a statistically 'real' or representative of the population. On the other hand a small sample size can generate a very strong correlation with a low p-value that is not statistically significant meaning the result is due to chance alone.
You should select the Degrees of Freedom option box on the calculator if your data sets have a wide spread of the data around the mean. Degrees of freedom = 2 means the number of pairs in your sample minus 2 (n-2). This reduces the variance and for statistical significance testing, brings your data closer to a normal (bell shape) distribution.
Always plot your data on a scattergraph and determine a trend line to get a visual feel for the strength of the correlation.
Spearman's Rank Correlation Coefficient
[1] Calculations based on exact critical p values for N >2 <=18 and very accurate critical values for N >18 <101 estimated using the Edgeworth approximation.
Spearman's Rank Correlation Coefficient Manual Calculation Examples

