Spearman's Rank Correlation Coefficient Rs and Probability (p) Value Calculator
The Spearman's Rank Correlation Coefficient Rs value is a statistical measure of the strength of a link or relationship between two sets of data. This calculator generates the Rs value, its statistical significance level based on exact critical probabilty (p) values[1], scatter graph, trend line and conclusion.
Spearman's Rank has many common uses in geography including the analysis of changes in economic, social or environmental variables over distance along a transect line, or questionnaires with Likert scales (e.g. a 7-point scale from 'strongly agree' through to 'strongly disagree').
The coefficient (Rs) is calculated on this calculator using the common formula:
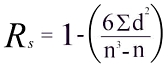
The answer will always be between 1.0 (a perfect positive correlation) and -1.0 (a perfect negative correlation). An Rs of 0 indicates no association between ranks.

We can describe the strength of the correlation using the following guide for the value of Rs[2]:
| The strength of a correlation | |
| Value of coefficient Rs (positive or negative) | Meaning |
| 0.00 to 0.19 | A very weak correlation |
| 0.20 to 0.39 | A weak correlation |
| 0.40 to 0.69 | A moderate correlation |
| 0.70 to 0.89 | A strong correlation |
| 0.90 to 1.00 | A very strong correlation |
To prove something using statistics, you should assume the opposite, that there is no correlation between your data sets. This is known as setting the null hypothesis (H0). Your hypothesis should always be stated in its null (H0) and alternative (H1) forms.
The p (or probability) value obtained from the calculator is a measure of how likely or probable it is that any observed correlation is due to chance. P-values range between 0 (0%) and 1 (100%). A p-value close to 1 suggests no correlation other than due to chance and that your null hypothesis assumption is correct. If your p-value is close to 0, the observed correlation is unlikely to be due to chance and there is a very high probability that your null hypothesis is wrong. In this case you must accept the alternative (H1) hypothesis that there is a correlation between your data sets. A guide to interpreting a p-value is shown below.
Interpreting a p-value
In geography, a p-value of 0.05 (5%) or less is typically considered statistically significant, as illustrated below:
|
||||||||||||||||||
In geography we work generally with a strong 5% probability level (p = 0.05). Above this level, your null hypothesis is considered correct. At or below this level, there is at least a 95% probability that your null hypothesis is wrong, that the data are statistically significant and that they show a true relationship. In this case, you must reject the null (H0) hypothesis and accept the alternative hypothesis (H1). In other words, a 5% (p = 0.05) probability level indicates statistical significance with at least 95 in every 100 researchers undertaking the same investigation expected to find a similar statistically significant correlation from their data analysis.
With a large sample size a very weak correlation Rs value can have a significant p-value. In this case, the weak correlation is not due to chance factors, but because with a large sample the low correlation is a statistically 'real' or representative of the population. On the other hand a small sample size can generate a very strong correlation with a low p-value that is not statistically significant meaning the result is due to chance alone.
Your minimum sample size should be at least 10. Below that point the Rs values are unreliable. A simple rule of thumb in statistics is that the absolute minimum number of observations should be at least five times the number of variables being correlated.
Degrees of freedom (df) are not needed unless you are testing significance levels using Student's t distribution.[3] Degrees of freedom = 2 means the number of pairs in your sample minus 2 (n-2).
Always plot your data on a scatter graph and determine a trend line to get a visual feel for the strength of the correlation.
Spearman's Rank Correlation Coefficient
[1] Calculations based on exact Two-Tail Probabilities critical p values for N >2 <=18 and very accurate critical values for N >18 <101 estimated using the Edgeworth approximation. Source: Philip H. Ramsey, 1989, Critical Values for Spearman's Rank Order Correlation, Journal of Educational Statistics Fall 1989, Vol 14, No. 3, pp. 245-253.
[2] Source: J. Fowler, L. Cohen and P. Jarvis, 2009, Practical Statistics for Field Biology, p. 132
[3] Source: S.Gregory, 1978, Statistical methods and the geographer, p. 188
Reporting Spearman's Rank Statistics in APA Format
Most universities today require students to follow APA format in the reporting of statistics and narrative as in the following example. Results of the Spearman correlation indicated that there was a significant positive association between river gradient and bedload long axes size, (rs[27] = .558, p < .001). The number following r in parentheses corresponds to the sample size. Then the Rs correlation coefficient is reported, followed by the p-value. Note that when a p-value is less than .001, we do not report p = .000. This is because p-values can never be equal to zero. P-values below .001 are reported as p < .001.
Spearman's Rank Correlation Coefficient Manual Calculation Examples


