Standard Deviation
What is the standard deviation?
The standard deviation is a statistic that tells you how tightly data are clustered around the mean. When the sizes are tightly clustered and the distribution curve is steep, the standard deviation is small. When the sizes are spread apart and the distribution curve is relatively flat, that tells you that there is a relatively large standard deviation.
What is a distribution curve?
There are, as is well known, lies, damned lies and statistics. And within statistics there is the bell curve. This is the shape of the frequency distribution one gets when conducting measurements of just about anything in the natural world.
It first came to prominence in the early nineteenth century when Adolph Quetelet, the Belgian Astronomer Royal, collected data on the chest measurements of Scottish soldiers and the heights of French soldiers, and found that when both sets of measurements were plotted they tended to cluster in a symmetrical shape around a mean. Or, less technically, most soldiers were in a height range fairly close to the average. The bell curve became so ubiquitous in measurements of natural phenomena that it was eventually christened the 'normal distribution', and it has conditioned our thinking about statistical data ever since.
The example below simulates how the random distribution of dropping balls creates a bell-curve. At first there does not seem to be any pattern but after a few minutes the stacks conform to the superimposed curve

|
| Randomly dropping balls create a normal distribution curve (bell curve) |
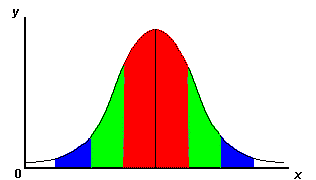 |
Normal distribution curve (bell curve)
|
Key to graph colours above |
|||||
| Colour | Standard Deviation | % of Population | |||
|
|
One standard deviation away from the mean in either direction on the horizontal axis | 68% | |||
|
|
Two standard deviations away from the mean | 95% | |||
|
|
Three standard deviations away from the mean | 99% | |||
Why is it useful? Smaller standard deviations reflect more clustered data. More clustered data means less extreme values. A data set with less extreme values has a more reliable mean. The standard deviation is therefore a good measure of the reliability of the mean value. The formula is as follows:
 |
Is there an easy way to calculate it?
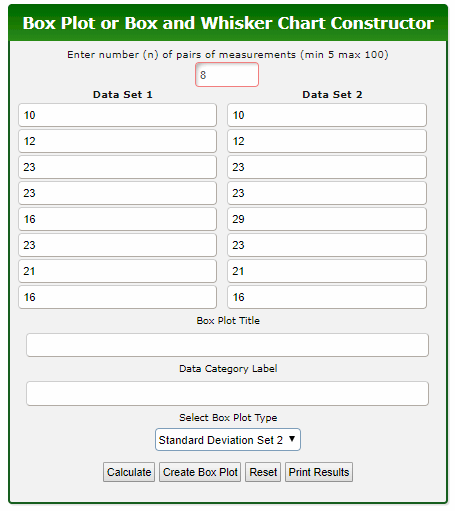
Our Box Plot Constructor has a standard deviation function as illustrated below.
 |
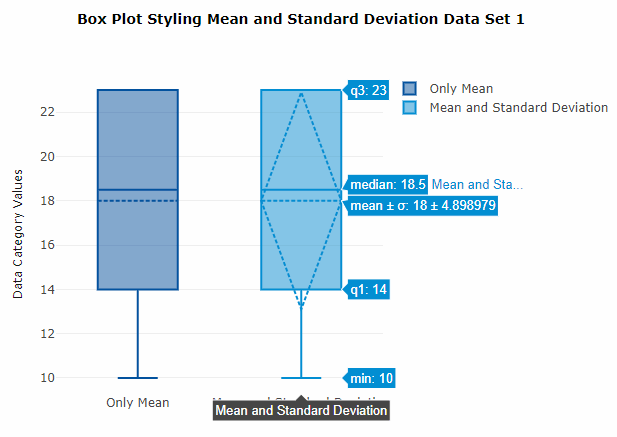 |
| Data Set 1 mean: 18.0; standard deviation: 4.898979 |
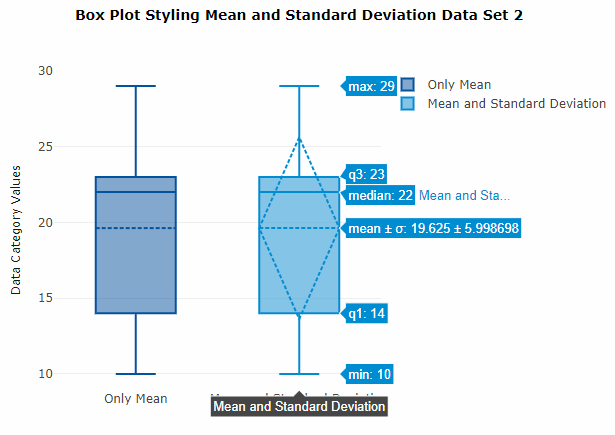 |
| Data Set 2 mean: 19.625; standard deviation: 5.998698 |
The Microsoft Excel programme will calculate the standard deviation and mean for a set of data listed in a spreadsheet column.
Method:
- List data set in a single column
- Click on the empty cell below the last data item
- Open INSERT menu > FUNCTION > STDEV > click OK
- The standard deviation is then shown and will appear in the empty cell.
- The excel screen example below is for a data set of 3 items
 |
What are its weaknesses?
The standard deviation does not take into account how close together the means are between two sets of data. The spread of data at two sample sites could have very similar standard deviations but very different means.
Which test can be used to show how close together are the means of 2 sets of data?
The Student 't' test.
